判决反馈均衡器(中)
判决反馈均衡器(下)»
Part4 瞬态波形和眼图
判决反馈均衡器DFE(上)章节中提到的不同结构,其瞬态波形会存在差异。其采样前的眼图直观反映了采样器的幅度Margin和CDR采样时刻的裕度。
为了对比,这里使用VerilogA理想模型,激励条件尽可能保持了一致。模型数据率为10GT/s,输入信号为800mVppd。信道插入损耗约为10dB@5Ghz,无CTLE,仅DFE补偿,2个Tap。通过信道后,采样前数据眼图如图1所示。

全速率直接反馈结构的瞬态相关波形和稳态眼图分别如图2和3。
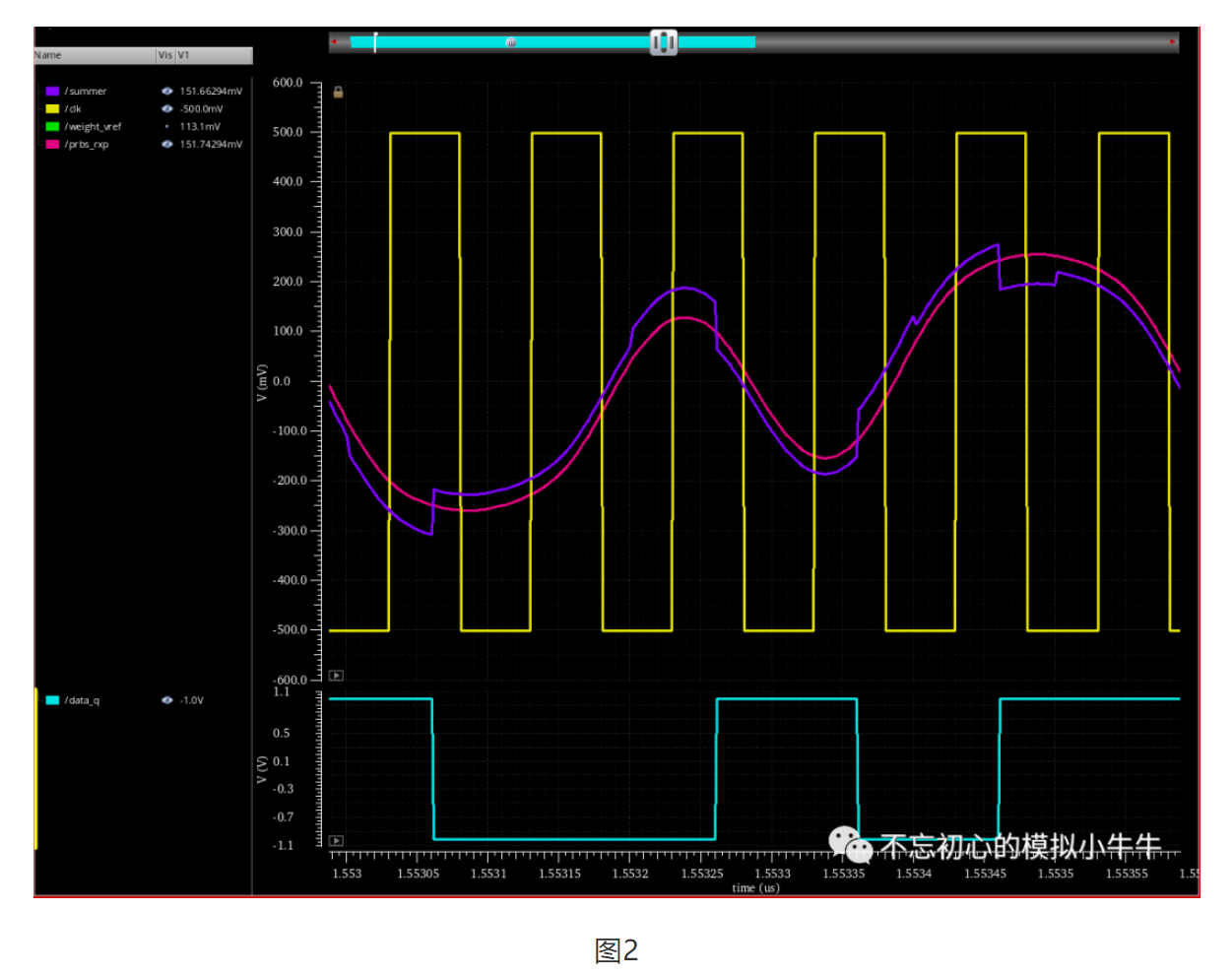
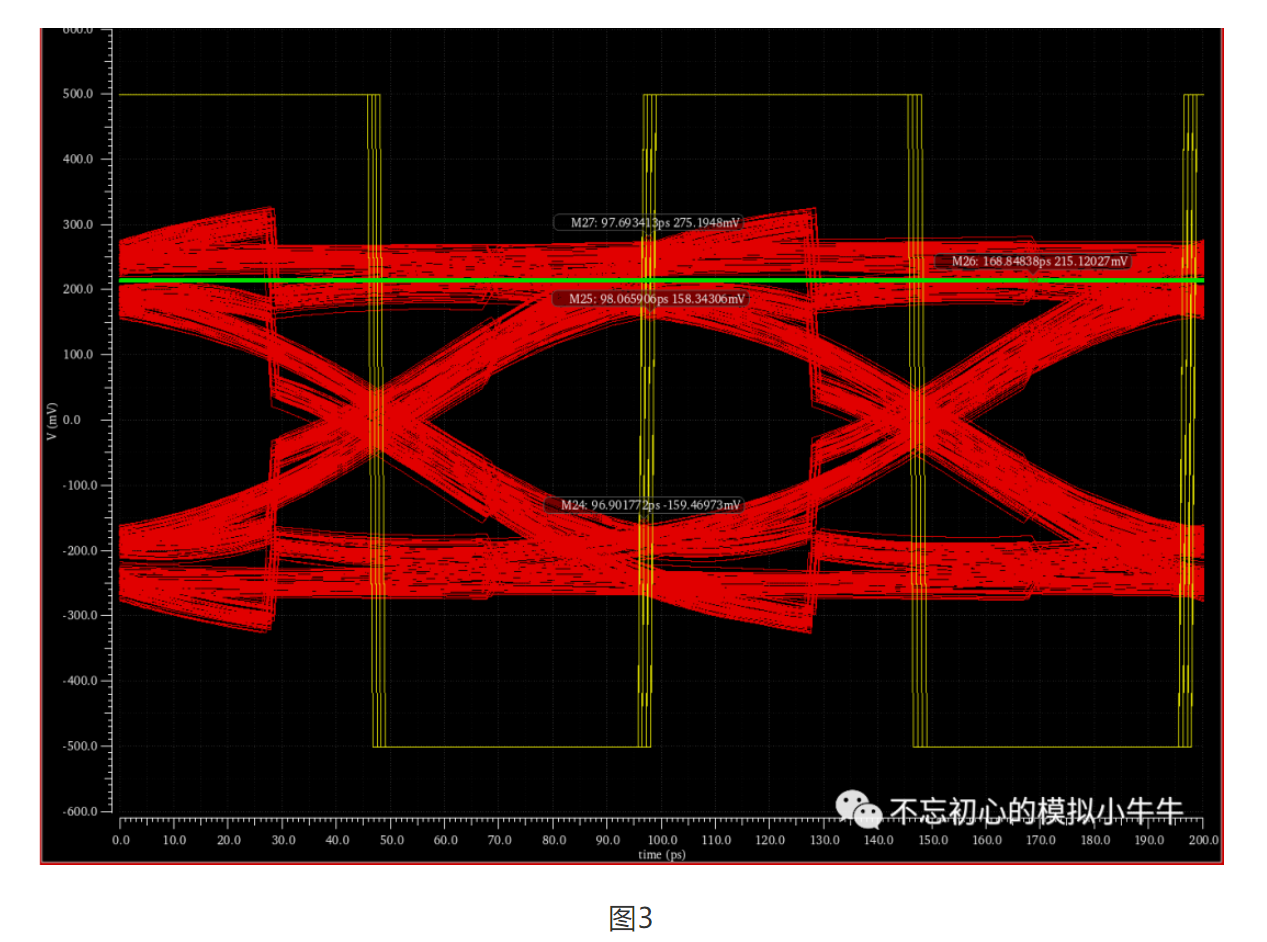
收敛过程如动图4所示。可以比较明显观察到dfe补偿作用会导致采样时钟发生前移。
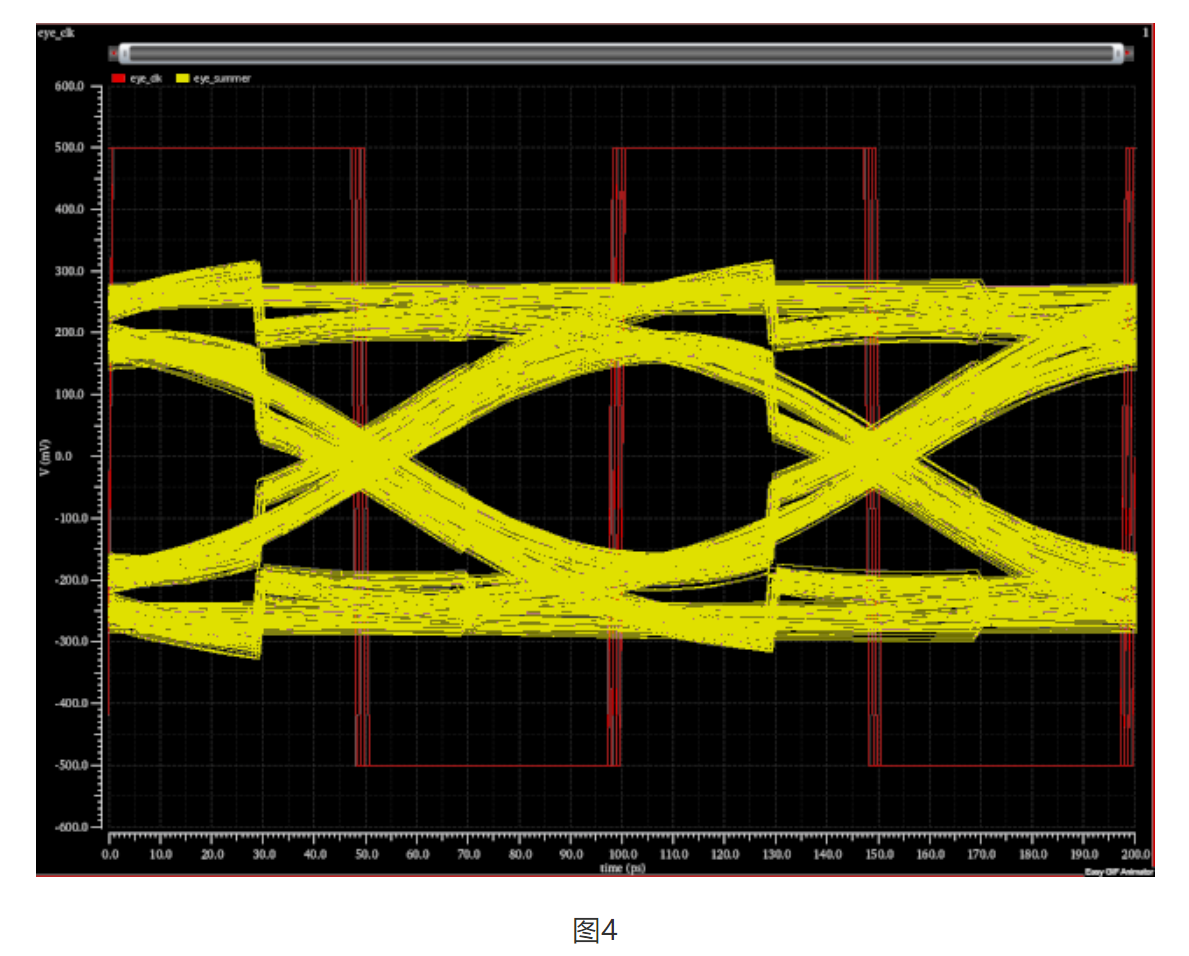
半速率直接反馈结构的瞬态相关波形和稳态眼图分别如图5和6。图5可以看到加法器输入和加法器奇偶输出波形,通过interleave方式交替采样。
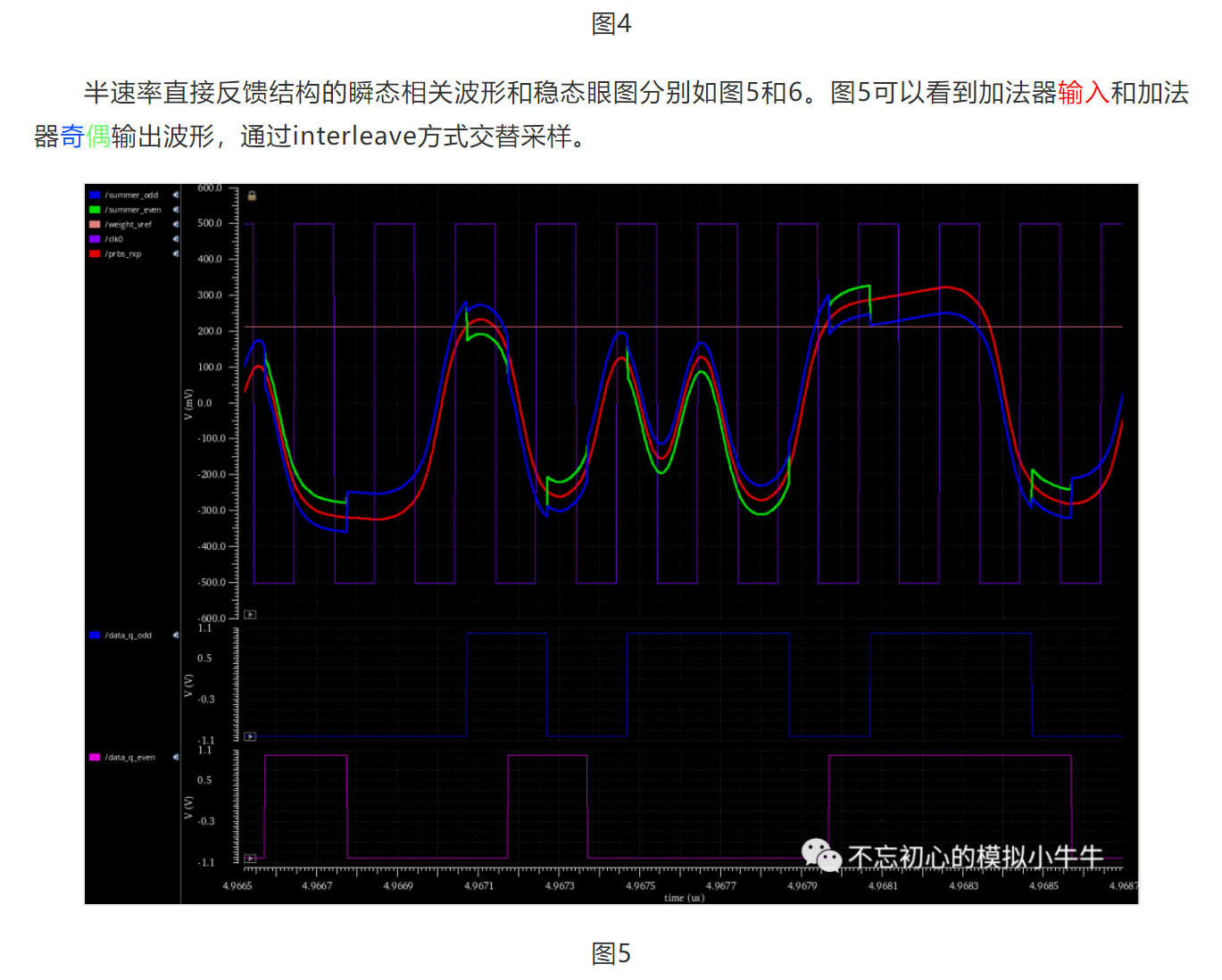
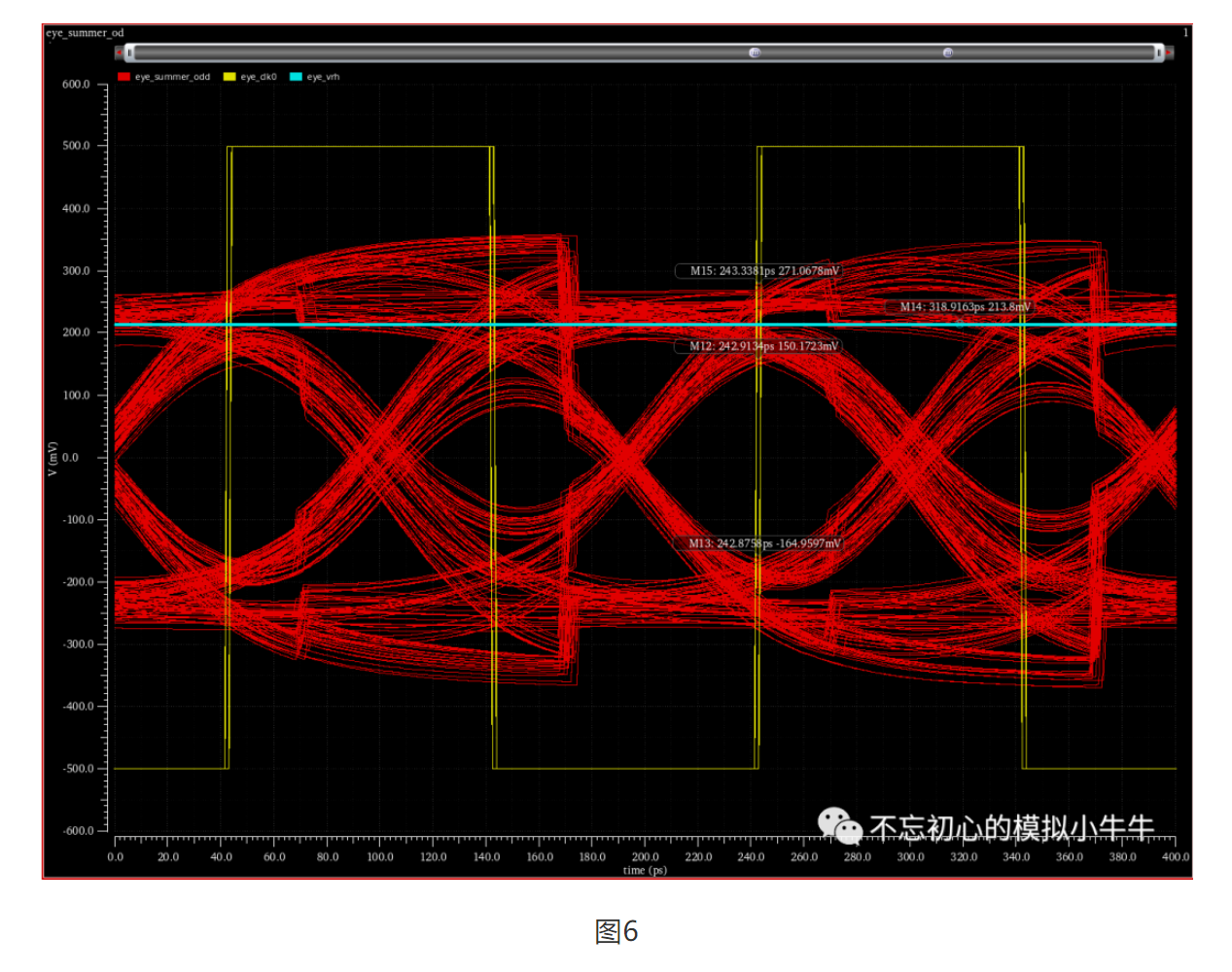
图7是奇偶路收敛过程的眼图。
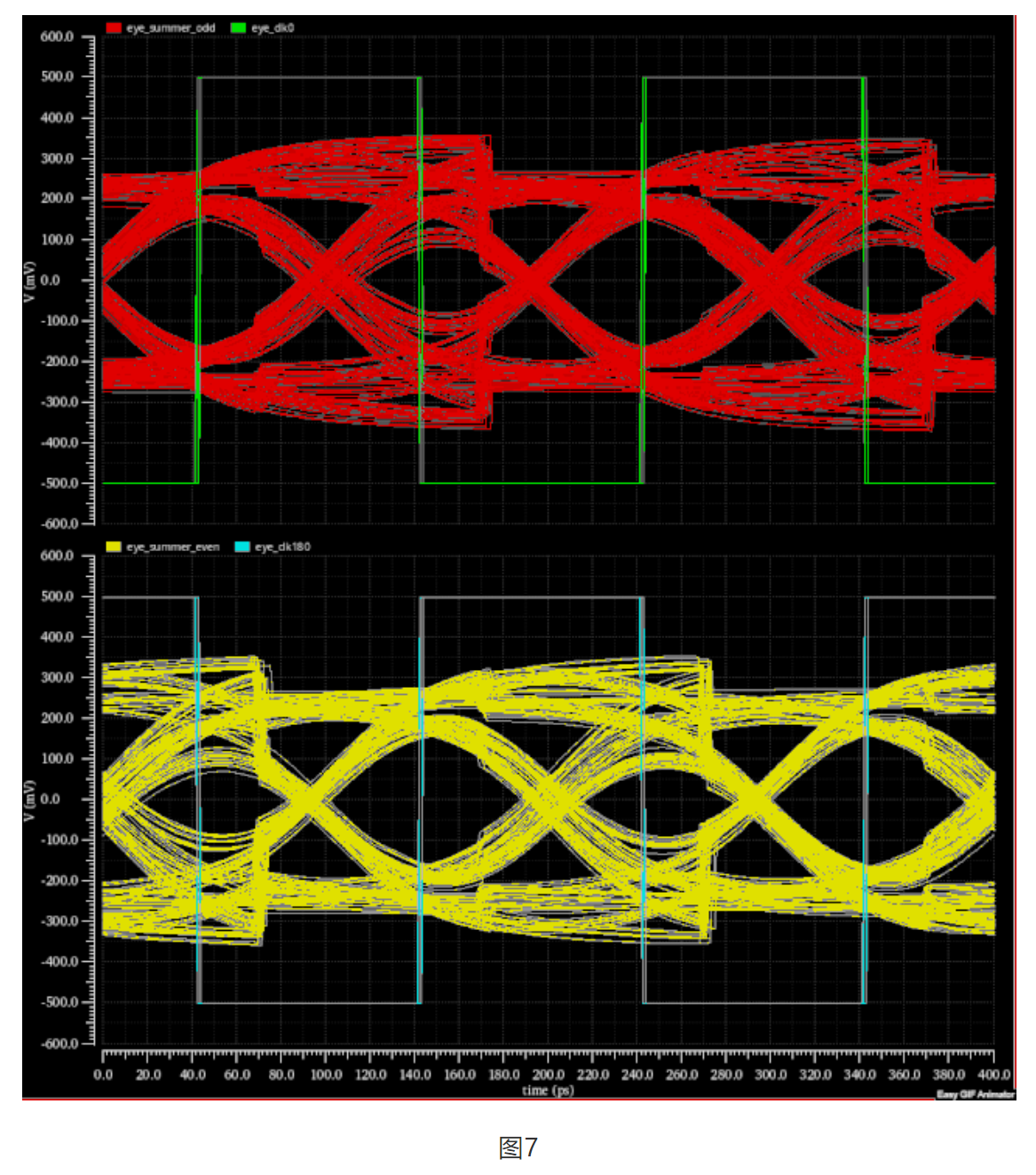
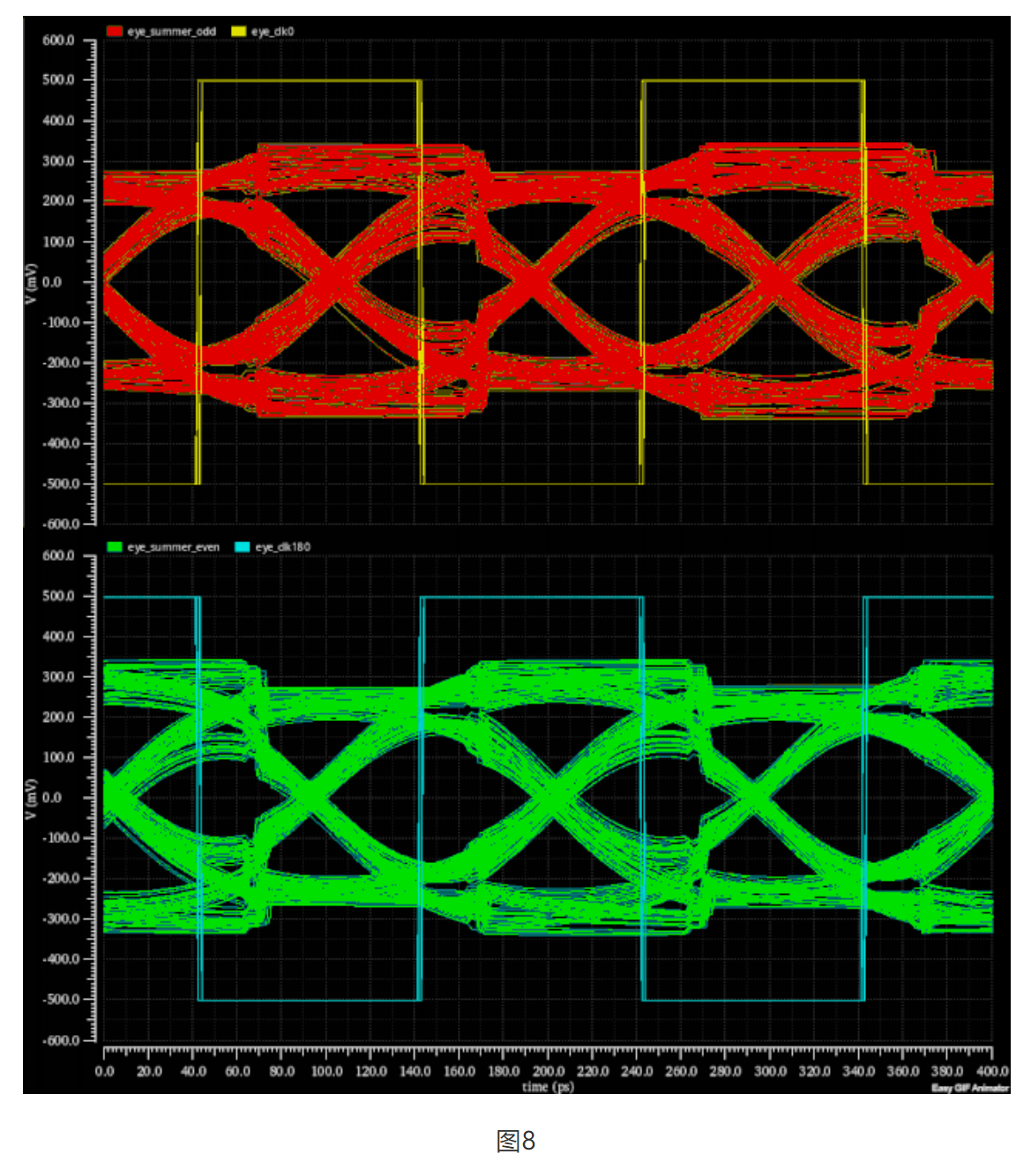
图8和图7一样,也是改进型半速率直接反馈结构的眼图,不知道大家能否看出差异?
对于预判式全(半)速率结构其瞬态波形和眼图和上述两种直接反馈结构类似,只是tap1分量没有在summer节点上体现,需要根据判断出的数据选择对数据进行tap1量的加或者减。
Part5 DFE对边沿的影响
传统2x过采样CDR,通过edge定位锚定data采样位置,edge位置的抖动和分布实际上会影响到data采样的裕量,特别是在比较大插入损耗的情况下,眼睛裕量本身就比较小。
前边一系列动图可以明显看到dfe对采样时钟的相位影响,随着各tap补偿量的逐渐增加,采样时钟相位在cdr的调节下,相位逐步前移。cdr相位锁定位置的变化,反应了dfe对边沿的影响。
图9简单说明了DFE Tap1量的加减对边沿的影响,实际边沿数据变化和数据pattern,Tap阶数,响应时间密切相关。对于1-0的数据转换,pattern类型为110,可以看到Tap1量导致边沿提前;而pattern类型为010,因为存在tap1量符号反向,对边沿的影响和Tap量响应时间相关。
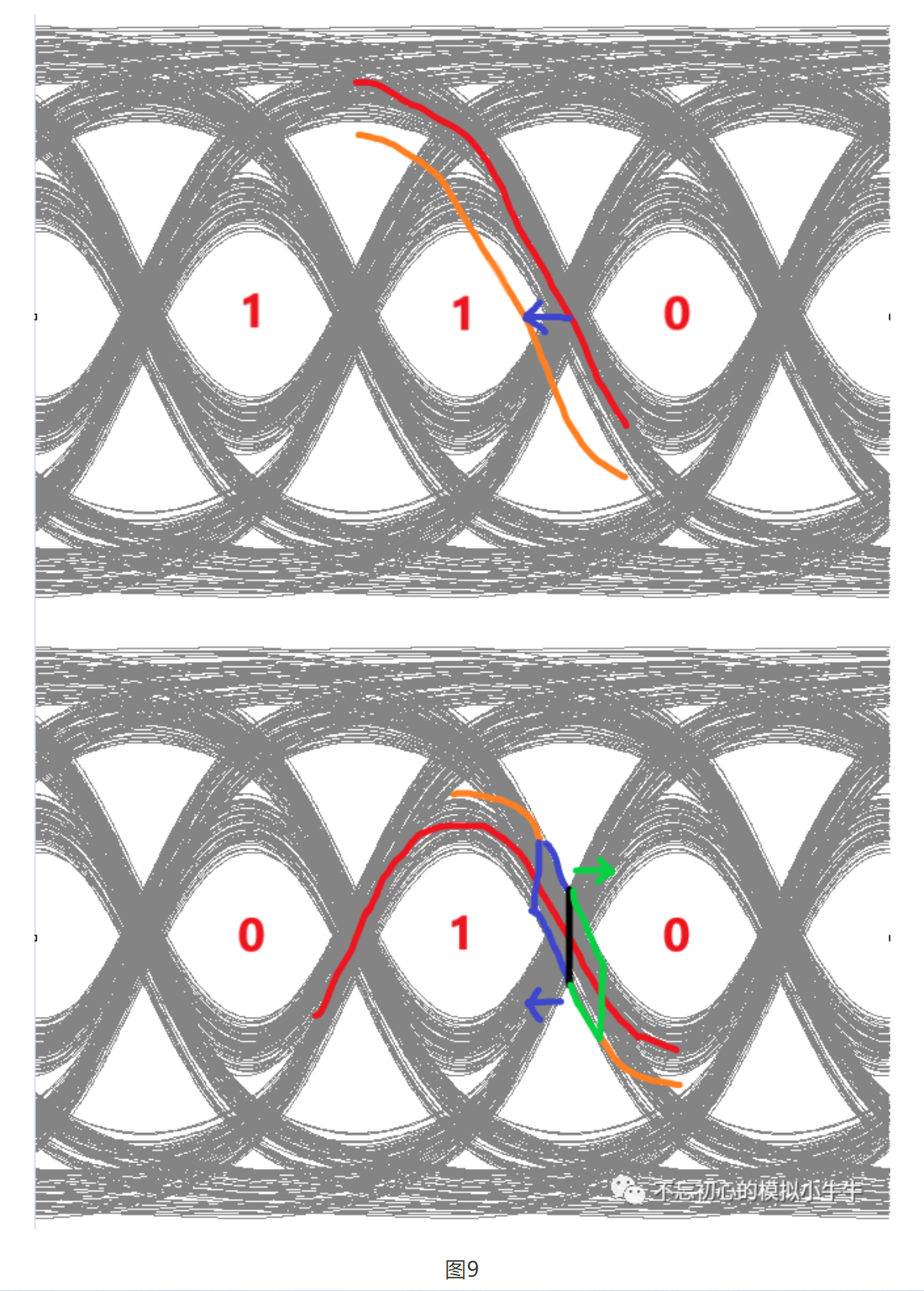
实际上,对于多Tap的DFE补偿,边沿包含了历史多位数据的影响。综合影响评估需要结合具体电路实现。
其实,最明显的边沿影响,是预判式结构。因为Tap1量加减处理是在summer之后。如果不对edge采样进行处理,锁定后的数据采样位置就会偏后。如图10所示。
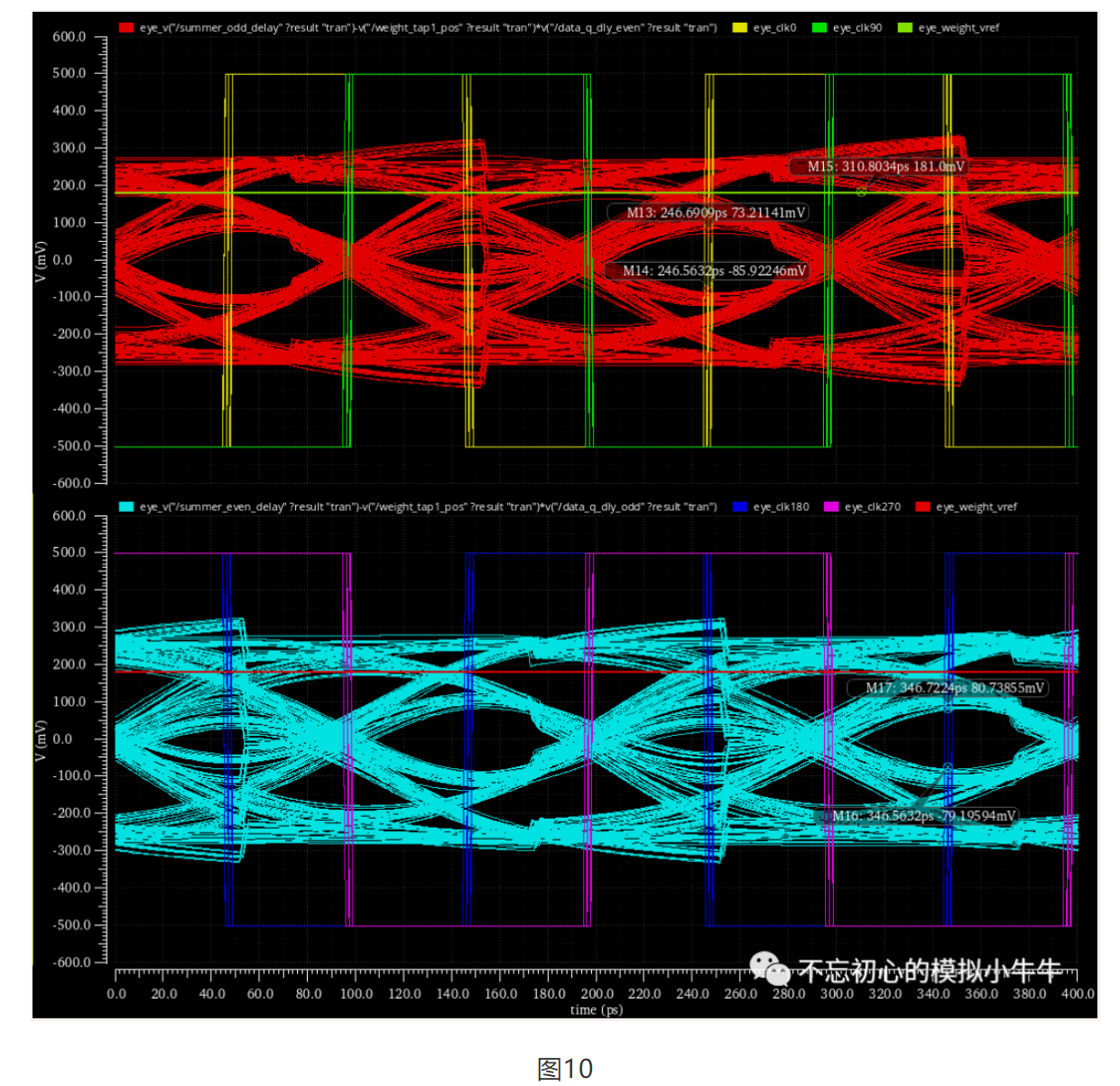
那么该如何解决这个问题呢?这里就留给大家做个思考吧。
图11是对edge补偿处理后的结果,可以看到等效的眼图收敛结果更优。

另外对2x过采样CDR时钟相位的影响。也需要考虑data和edge的先后顺序,和具体电路实现结构密切相关,具体哪种顺序更优,需要仔细评估。
这里总结下几种结构理想情况DFE收敛值情况,仅供参考。

最后送上,用Matlab工具SerDes Toolbox计算的结果合成的封面图的近似收敛过程。
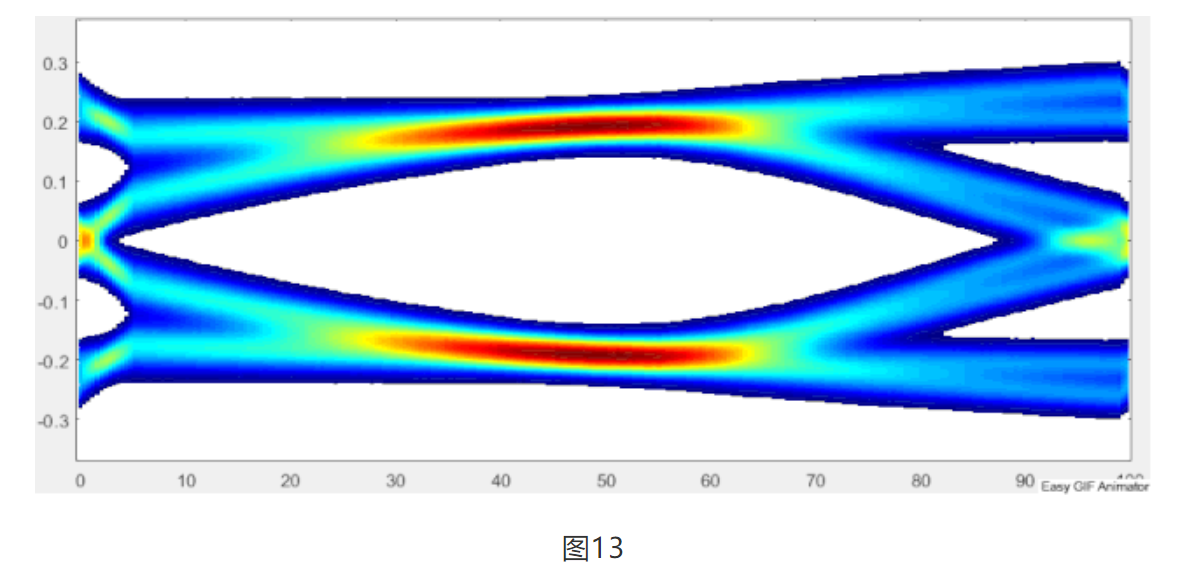
Part6 自适应算法简介
目前,自适应滤波器理论已经非常成熟,在通信和消费领域也有着广泛的应用。例如信道均衡,波束成形,噪声消除等。如图14所示。
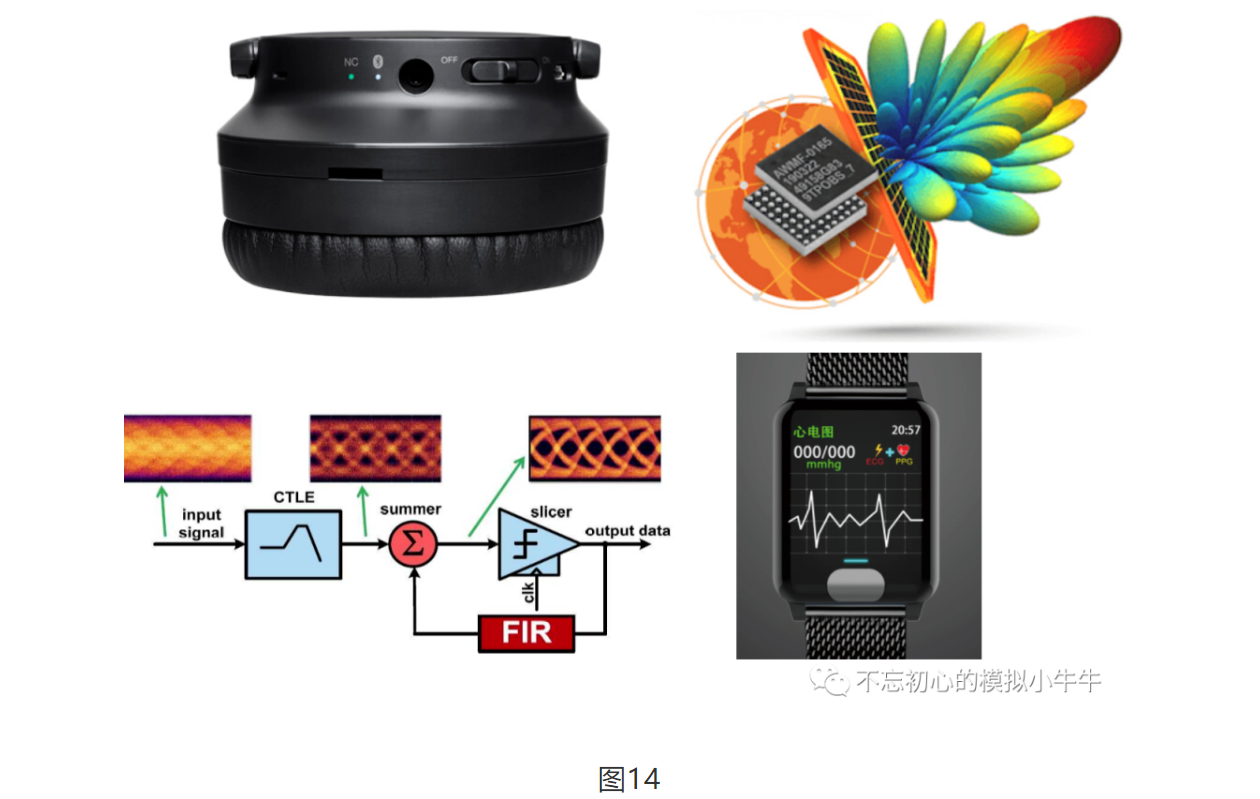
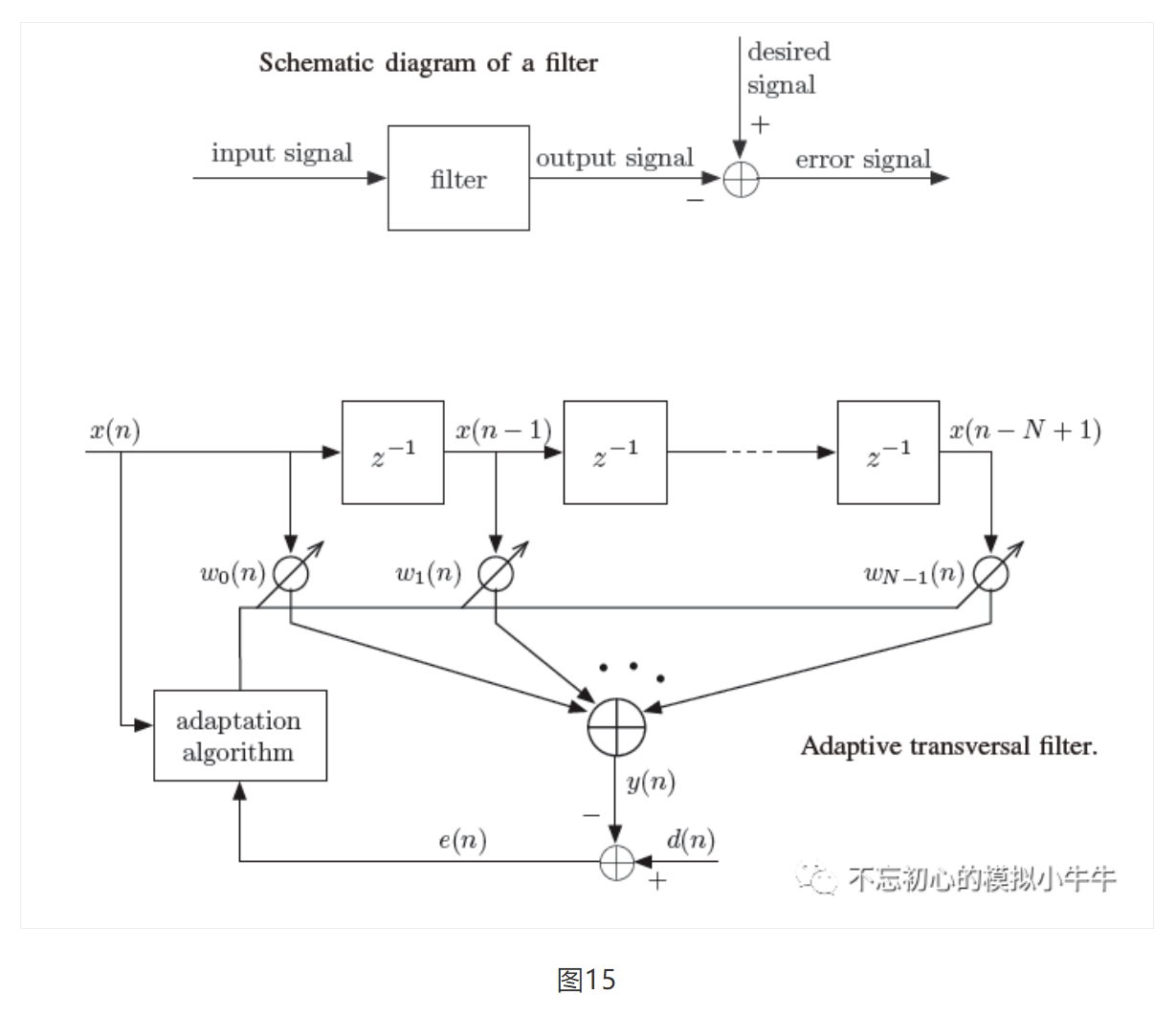
自适应滤波器如图15,简单来讲,就是通过调整滤波器,使滤波器输出信号和目标信号接近或者相等。主要是(非)线性离散时间系统对离散信号的处理。通常使用性能函数(Performance Function),评估不同滤波器系数的性能。比如用误差信号的均方误差(Mean-Squared Error,MSE)。最小均方误差的滤波器,又称之为维纳滤波器(Wiener Filter)。各种自适应算法就是要得到滤波器的维纳解(Wiener Solution)。
在通信领域,自适应滤波器主要用作信道均衡(Channel Equalization),如图16所示。图中信道H(z)是信道传递函数。噪声v(n)可以看做是串扰及噪声等非理想因素的组合。图中均衡器W(z)就是要消除码间干扰,降低串扰和噪声影响的自适应滤波器,均衡器输出y(n)需要满足量化输出的数据在规定的误码率范围内。
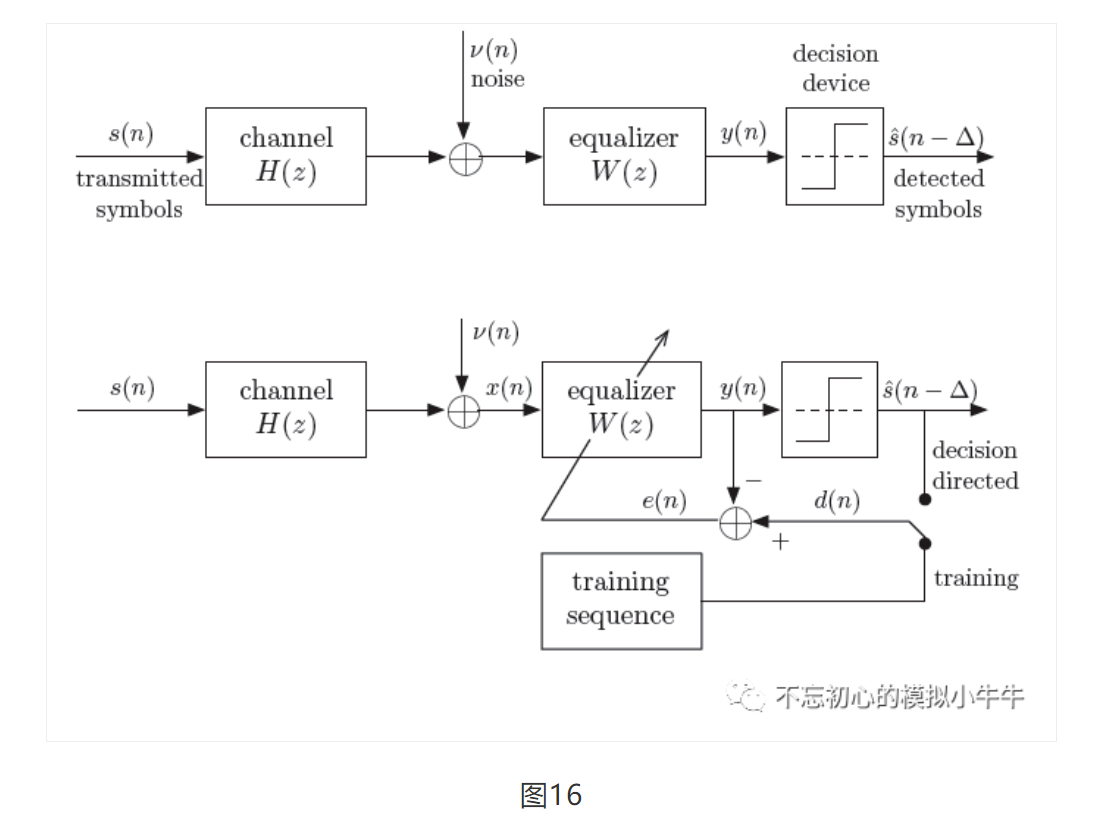
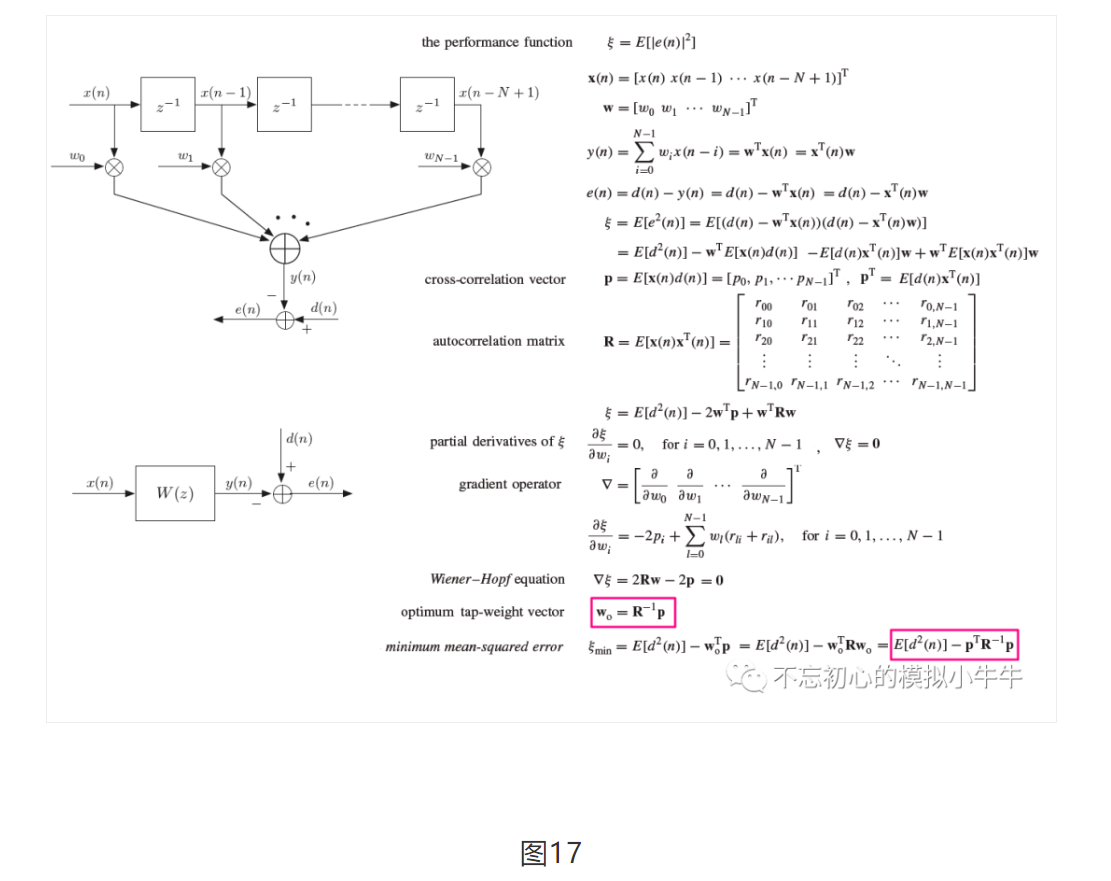
图17是维纳滤波器的数学推导1,滤波器系数满足维纳-霍普方程,维纳解形式包含输入数据自相关矩阵R,输入数据和目标数据的互相关向量p的关系。可以看到维纳解是可以一步到位,但会涉及比较复杂的矩阵运算量。
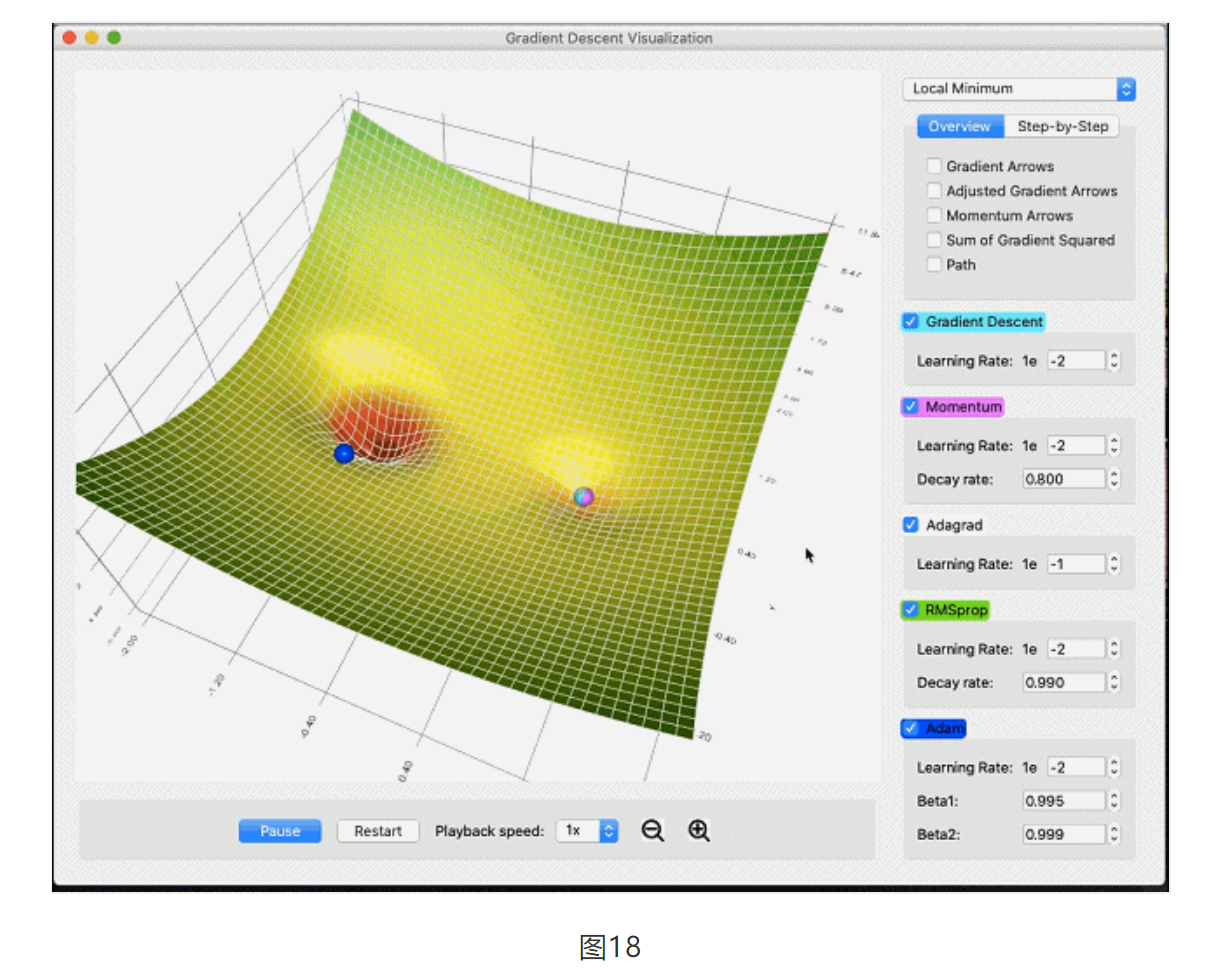
另一种方法通过迭代搜索算法,从任意一个Tap权重向量wi,逐步迭代收敛到最优权重向量wo。这里就要提到基于梯度的最速下降法(method of steepest descent)。图18[2]给出个动画,还是比较形象的说明了梯度下降法,整个性能误差面一定会存在最低点(可能包含多个局部最低点),这个点也就是维纳解的位置。
基于梯度的最速下降示意图及推导过程如图19所示。可以看到基于梯度的最速下降法能够以最快的方式按照负梯度方向,朝着维纳解位置运动。同时,迭代步长增益μ和自相关矩阵R的特征根λi需要满足一定的关系从而保证收敛过程的稳定性。

图19中基于梯度的最速下降法还是需要知道自相关矩阵R和互相关矩阵p。计算过程还是比较复杂。我们知道前述梯度是误差平方期望的梯度,如果我们用瞬时误差梯度代替期望误差梯度,则可以简化迭代过程为LMS算法实现,如图20所示。
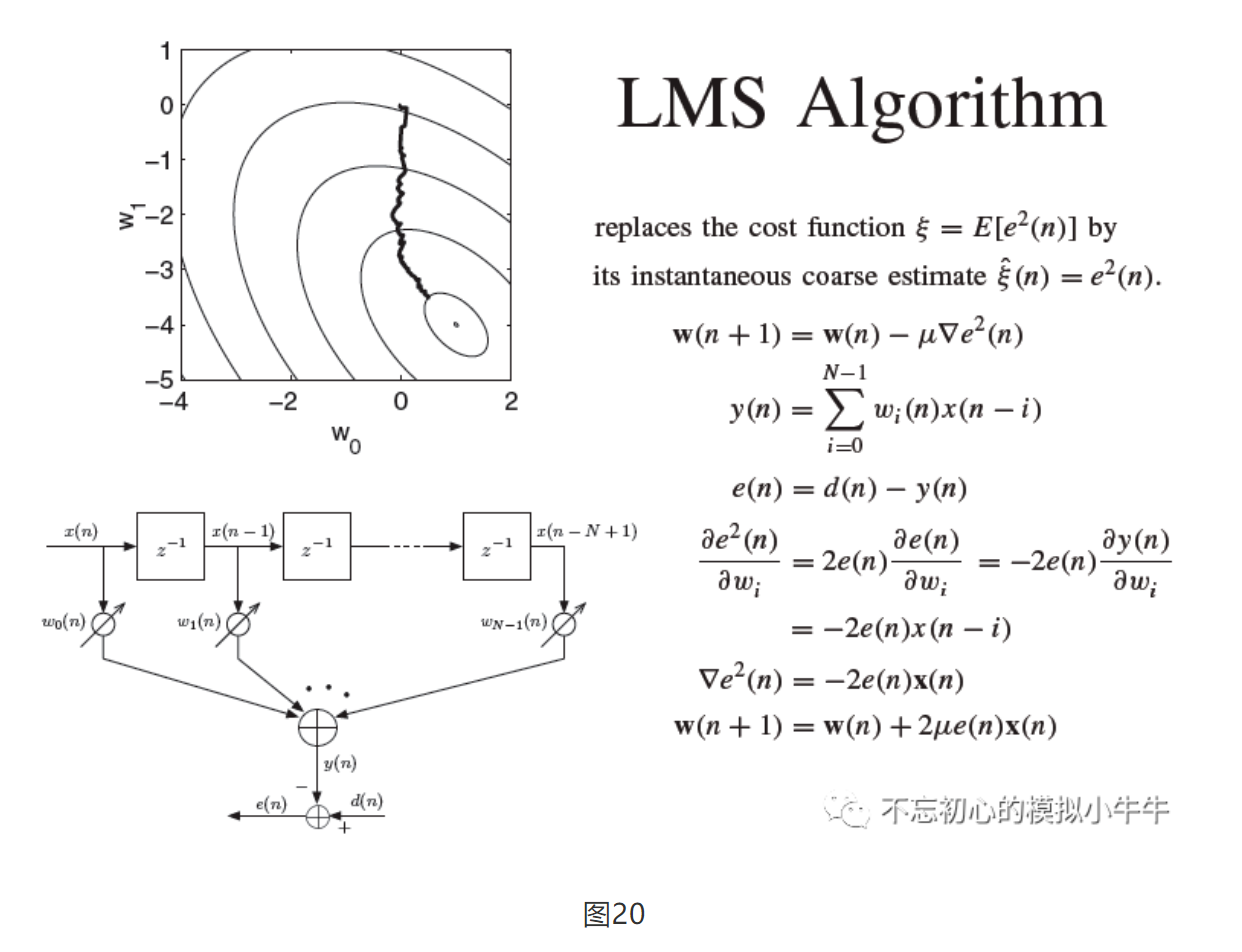
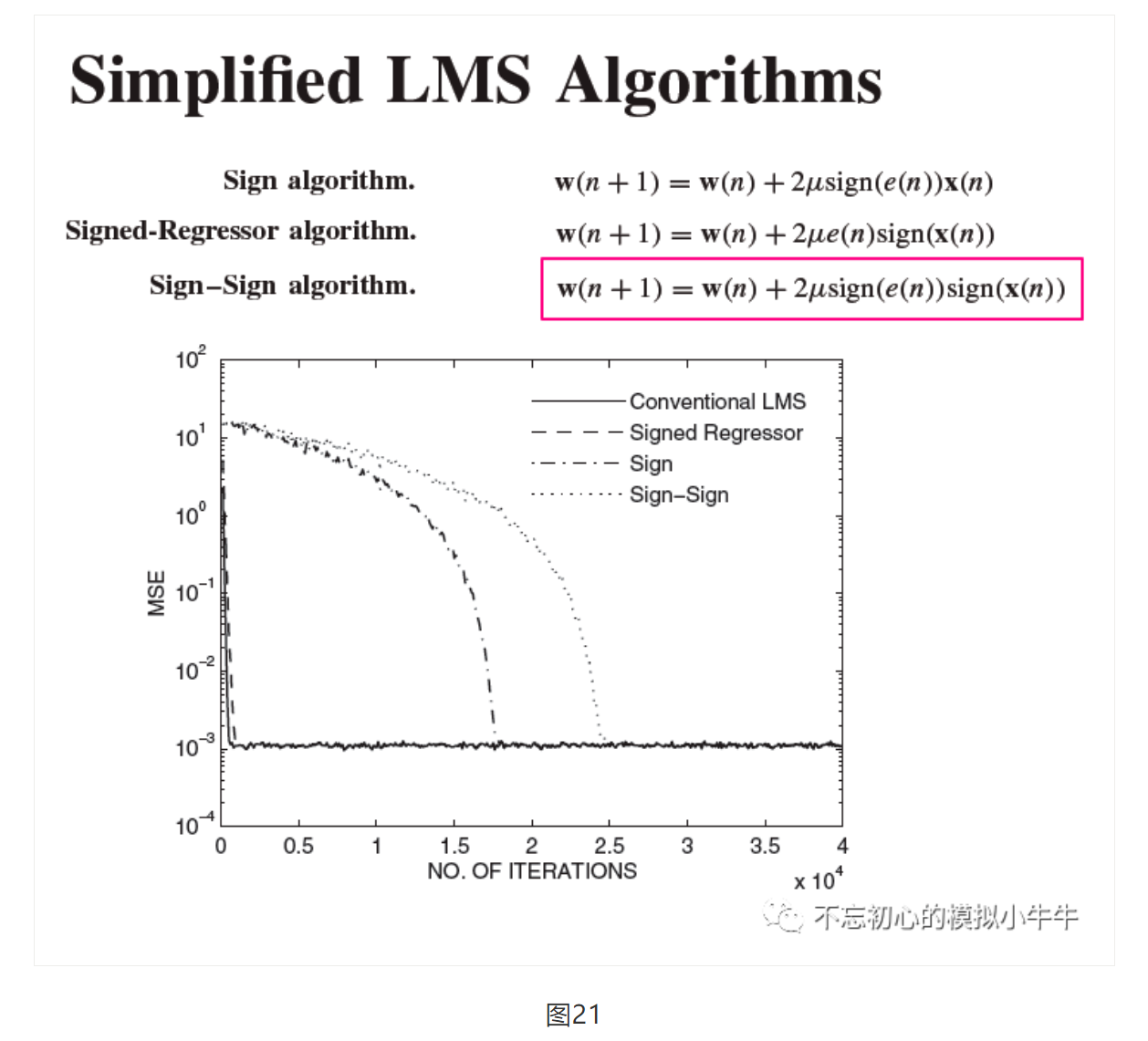
图20的LMS迭代过程使用了瞬时误差e(n)和历史数据矩阵**x(n)**。还是会涉及到浮点运算(乘法和加法)。运算硬件消耗也是比较大。于是就有了图21所示的简化版本。主要是误差或者历史数据的符号化。可以不同程度简化计算复杂度。不过图中也可以简化计算的代价是收敛时间,还有可能残余更大的均方误差MSE。
判决反馈均衡器(Decision Feedback Equalizer,DFE),正如其名字所示,需要通过历史判决值,构成反馈FIR滤波器,对输入信号进行补偿。如图22所示。需要注意的是,图中Tap反馈到加法器为负,也就是实现减法。同时误差信号的定义和前述基本滤波器定义也是相反的。负负为正。因此权重迭代表达式符号也和前述结果相同。
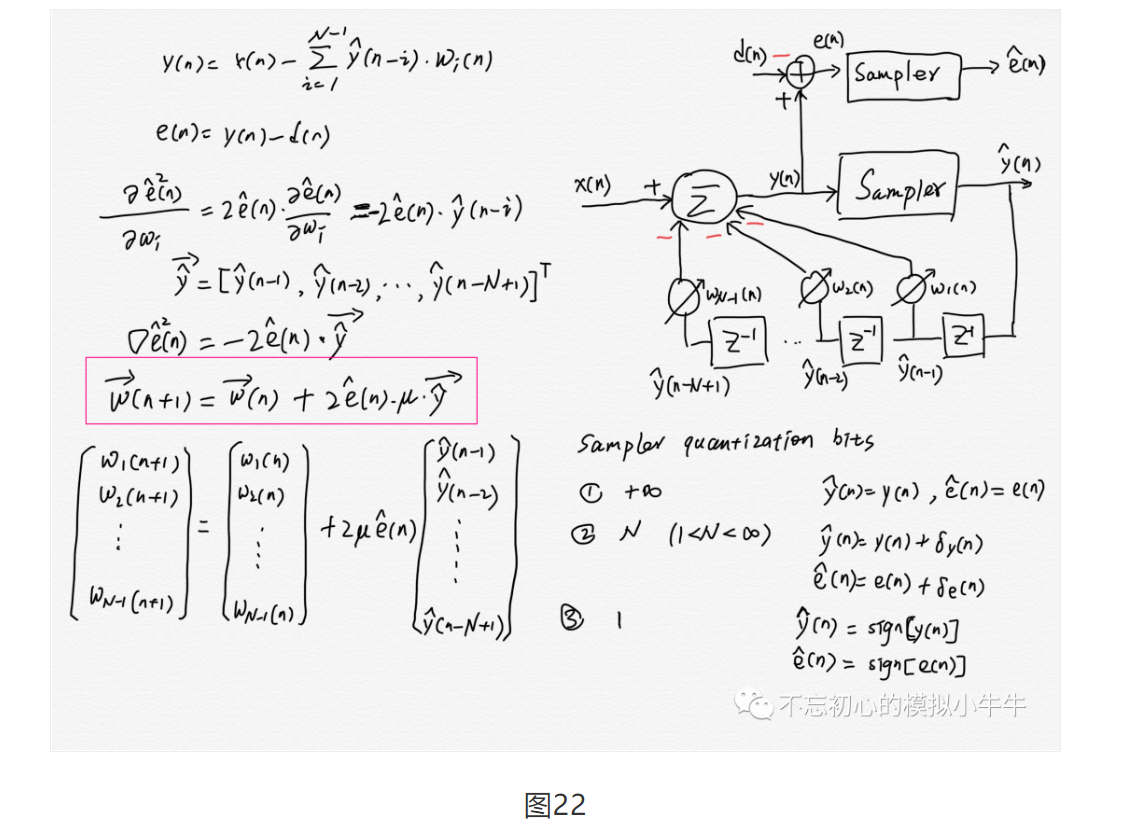
图22中当采样器量化精度为1bits时,就实现图21中sign-sign LMS,实际电路实现时,通过分时复用和模版数据选择,可以进一步降低硬件实现成本。
当滤波器收敛后,tap系数趋于稳定。滤波器输出值和输入数据及量化误差的传递函数如图23所示。
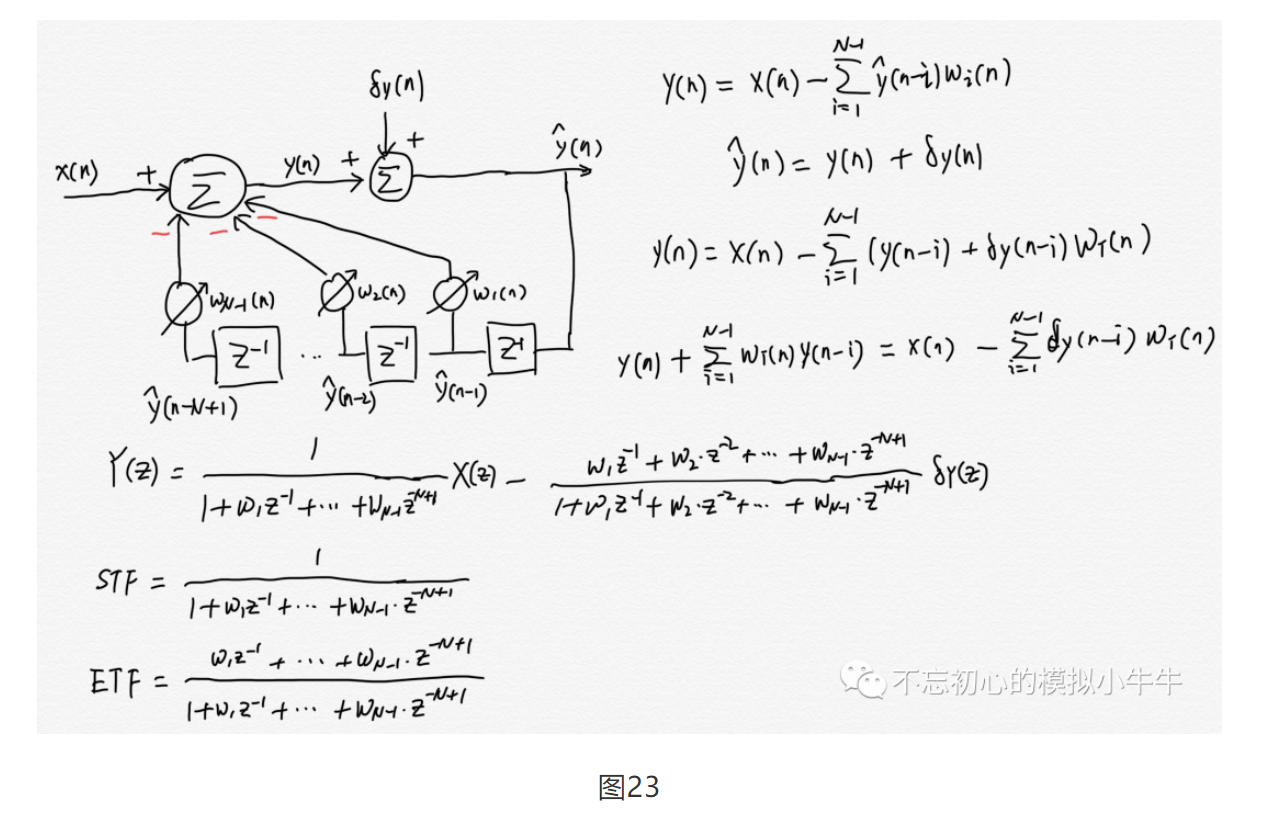
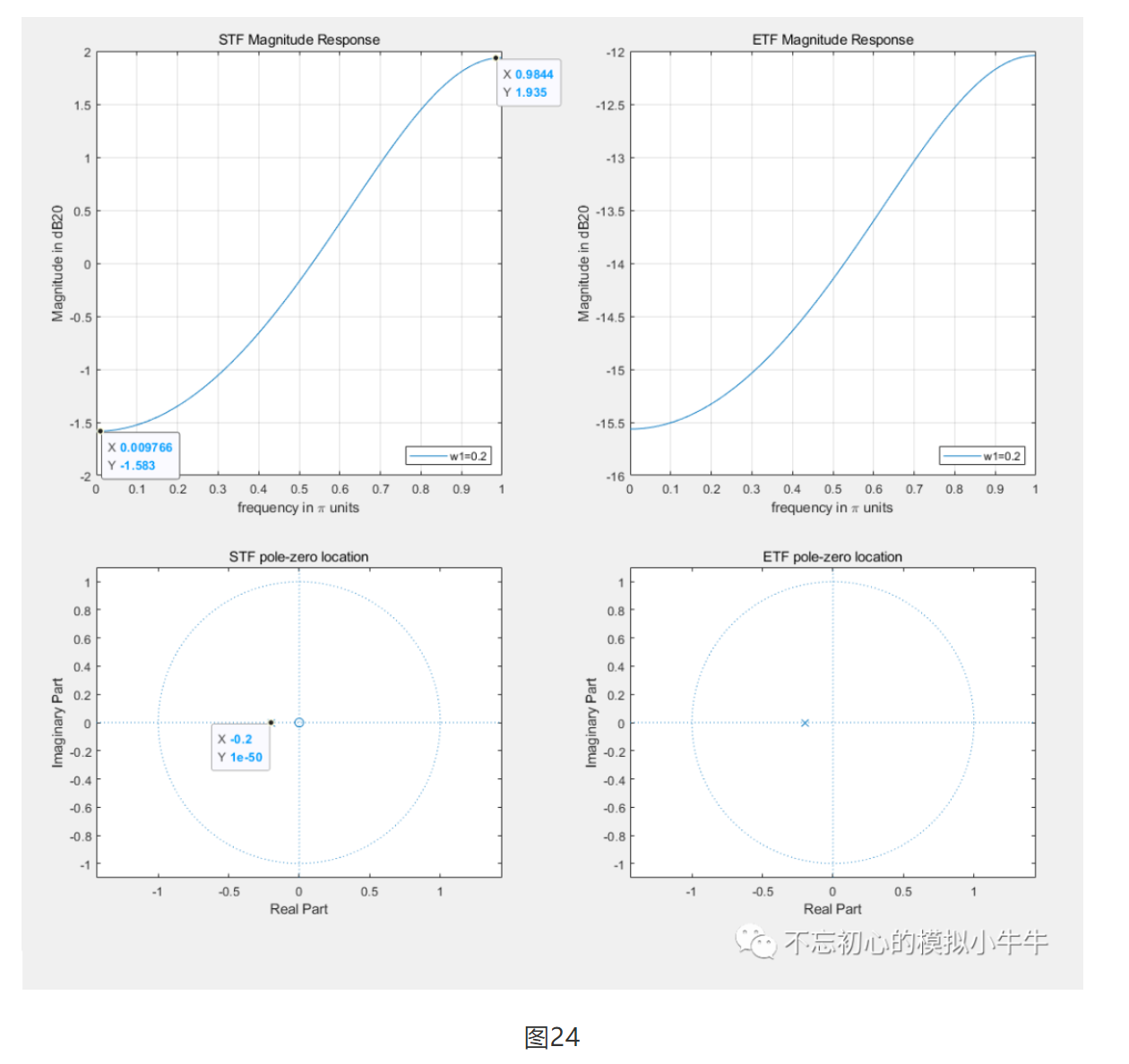
图24是简单的一阶DFE传递函数及零极点分布,可以看到信号传递函数是高通(高阶DFE频响特性不一定具有全频段的高通特性),衰减低频,提升高频。从而补偿输入数据的拖尾。误差传递函数整体增益是衰减的。